De nombreux articles et recommandations ont spécifié le protocole qu’il convient de respecter pour faire une revue systématique de la littérature. (Systematic reviews: CRD’s Guidance for undertaking reviews in health care, 2009), (Cochrane Handbook for systematic review, 2008). Ces règles comportent sept étapes:
- Structuration d’une question unique sur la base des critères PICOS : « P » population cible ; « I » nature de l’intervention ; « C » comparateur choisi ; (O) « outcomes » retenus comme critères de jugement ; (S) schémas d’étude à privilégier ;
- Formulation ex ante des critères d’éligibilité et de non-éligibilité des études au regard des critères choisis ;
- Choix des bases documentaires à interroger (deux au moins) et délimitation de la période d’analyse. A interroger en première intention les bases MEDLINE, EMBASE et The Cochrane Central Register of Controlled Trials ;
- Identification des descripteurs correspondants (CISMef, EMTREE, MESH ou autres) et écriture des équations de recherche;
- Sélection sous END Notes, élimination des doublons, sélection sur titres et abstracts ; double lecture intégrale des articles ; construction du diagramme de flux ;
- Évaluation de la qualité des études (validité interne-externe) ;
- Extraction des données selon une grille standardisée définie a priori.

Les méta-analyses par paire permettent d’augmenter la puissance des essais cliniques et de synthétiser leurs résultats de façon quantitative lorsque les options thérapeutiques font l’objet d’une même comparaison face à face dans plusieurs essais différents. Deux types de modèles peuvent être mis en œuvre dans le cadre d’une méta-analyse.
Dans un modèle à effets fixes, on suppose que chaque étude estime le même paramètre sous-jacent. Autrement dit, la variabilité observée entre les effets estimés dans chaque étude ne provient que de la précision avec laquelle les effets sont mesurés. Dans ce cas, l’effet global du traitement correspond à la moyenne pondérée des effets estimés dans chaque étude, les poids associés étant égaux à la précision avec laquelle les effets sont mesurés.
Les modèles à effets aléatoires prennent au contraire la variabilité inter-études. Dans ces modèles, on abandonne l’hypothèse selon laquelle chaque étude estime exactement le même effet. En revanche, on suppose que chaque étude estime un effet différent, mais que tous ces effets sont issus d’une même distribution d’effets.
La description ci-dessus des modèles à effets fixes et à effets aléatoires se place dans un contexte classique, fréquentiste, c’est-à-dire que les paramètres sont supposés fixes et inconnus. Dans un paradigme bayésien, au contraire, les paramètres sont supposés aléatoires, ce qui permet d’associer une distribution de probabilité sur chacun d’entre eux.

Les essais présentés en commission de la transparence n’ont pas toujours le bon comparateur. S’ils ont été mis en place en Amérique du Nord, il peut s’agir d’un simple placebo ou des traitements usuels de référence sans que les résultats spécifiques de chacun d’entre eux soient isolés. Lorsque le ou les comparateurs sont des traitements actifs, leur nombre dépasse rarement deux ou trois. Ils ne permettent pas d’identifier les avantages et les inconvénients d’un nouveau traitement par rapport à l’ensemble de l’arsenal thérapeutique existant Trois méthodes permettent d’y procéder : les « rabouttages naïfs » à proscrire, les comparaisons indirectes ajustées sur un dénominateur commun, les mélanges de comparaisons directes et indirectes de traitements (MTC). Dans les modèles de mélange de comparaisons de traitements, on travaille toujours sur les différences d’effet par rapport à un comparateur commun mais cette fois le comparateur commun est choisi par l’analyste lui-même puis utilisé comme numéraire dans des rapports de cotes dont le numérateur et le dénominateur sont définis au regard du même traitement de référence. Il suffit alors de prendre le logarithme népérien du rapport de cote pour transformer le quotient en simple différence de logarithmes de côtes, ce qui permet de faire jouer les propriétés de transitivité. L’ensemble des essais peut être mobilisé, en comparant les traitements soit directement (en face à face) ou soit indirectement (par transitivité) sans « briser la randomisation » effectuée dans les essais de départ.

Les modèles de partition de la survie globale sont un cas particulier des modèles multi-états. Il s’agit de modèles de Markov à temps continu non homogène dont les probabilités de transition d’un état vers un autre ne sont pas nécessairement constantes au cours du temps. Le modèle tire son nom des travaux conduits dans les années 1993 par Gelber et Cole (Gelber et al., 1993a) qui ont décomposé la survie globale en trois phases : la phase thérapeutique avec les effets secondaires du traitement, la phase libre de tout symptôme et toxicité (TWiST) et la phase de rechute.
Dans le cadre du Q-TWiST standard, les informations correspondantes sont exclusivement documentées à partir des résultats observés dans les essais cliniques. Dans le cadre du Q-TWiST dit extrapolé, ces mêmes informations documentées sur une courbe de Kaplan Meier sont combinées avec une fonction de survie paramétrique pour extrapoler ces résultats à toute la vie. Le plus souvent les formes fonctionnelles adoptées donnent naissance à des probabilités de transition qui évoluent en fonction de la longueur du suivi et/ou en fonction du temps passé dans les différents états. Les modèles qui sont construits sur ces bases sont désignés sous le nom de modèles semi-markoviens pour les différentier des processus markoviens traditionnels dont les probabilités de transitions sont indépendantes de la durée totale du suivi et du temps passé dans l’état. Les modèles semi-markoviens généralisent les modèles de Markov puisqu’ils sont non homogènes et puisqu’ils permettent de définir explicitement les temps de séjour passés dans les différents états. Les probabilités de transition peuvent être calculées directement à partir des formes fonctionnelles utilisées.

L’adoption d’un horizon temporel vie entière est recommandée, car elle permet la prise en compte de toutes les retombées du traitement innovant par rapport à son comparateur aussi bien en termes de coûts qu’en termes de bénéfices cliniques quel que soit le moment de leur apparition, que ces retombées soient immédiates ou différées. Elle permet notamment permet de raisonner en termes d’espérance de vie et de délai moyen de survie globale. Les formes fonctionnelles spécifiques qui peuvent être retenues pour extrapoler les courbes de survie sans progression et de survie globale au-delà de la période de suivi de l’essai ont un impact significatif sur les résultats du modèle pour chacun des traitements analysés. Par conséquent, les distributions paramétriques doivent être sélectionnées sur la base d’un processus rigoureux pour éviter les biais. Ces distributions doivent, pour obtenir des projections vie entière acceptables, non seulement s’ajuster à court terme de façon satisfaisante aux données observées, mais il est nécessaire qu’elles fournissent aussi à long terme des résultats plausibles sur le plan clinique (Latimer, 2013).Voir la présentation

Les variables de coûts requièrent des méthodes d’analyse particulières. En effet, que ce soit pour l’estimation du coût d’une thérapie ou la comparaison des coûts dans deux groupes de traitement, les techniques statistiques applicables en général aux variables quantitatives ne s’appliquent pas. L’existence de valeurs extrêmes (les patients ayant eu de nombreuses complications engendrent des coûts beaucoup plus élevés que la moyenne) interdit ainsi l’utilisation de la moyenne arithmétique pour l’estimation d’un coût et du test de Student pour la comparaison de coûts (l’hypothèse de normalité requise est mise en défaut par la présence de ces valeurs extrêmes). Aucune méthode d’analyse n’est en fait communément acceptée pour le moment. Prenons l’exemple de la comparaison des coûts.
Tandis que certains auteurs prônent le test de Student car il a l’avantage de comparer les coûts moyens, d’autres défendent les techniques non paramétriques telles que le test de Mann-Whitney ou l’analyse du logarithme des coûts. Dans le cas du test de Mann-Whitney, ce sont les distributions de coûts qui sont comparées et non les valeurs moyennes. L’avantage est que l’on ne fait aucune supposition sur la nature de la distribution des coûts, mais l’information résultante est peu adaptée au problème posé. Dans le cadre de l’analyse sur le logarithme des coûts, l’hypothèse est que la distribution des coûts est log-normale. Si tel est véritablement le cas, il est possible d’obtenir, par une transformation inverse, un estimateur efficace de la différence de coûts. Dans le cas contraire, l’estimateur résultant n’est même pas convergent et la comparaison des coûts est complètement faussée. Chacune de ces trois méthodes possède donc des défauts majeurs. La technique de bootstrap non paramétrique est une alternative possible : avec cette technique, ce sont bien les coûts moyens qui sont comparés et aucune distribution n’est spécifiée a priori.

Le bootstrap non paramétrique a de multiples applications. L’une d’elles consiste à estimer la moyenne d’une variable sur un échantillon présentant des individus aux valeurs extrêmes. La technique de bootstrap est itérative. Pour cet exemple, la première étape consiste à tirer aléatoirement avec remise n individus parmi les n formant l’échantillon initial. A chaque tirage, chaque individu possède une même probabilité de figurer dans l’échantillon de bootstrap égale à 1/n. La seconde étape consiste à calculer la moyenne empirique sur l’échantillon de bootstrap. Ces deux étapes sont ensuite répétées un grand nombre de fois, typiquement 5000 ou 10000. Les 10000 moyennes empiriques fournissent alors une approximation de la distribution de la vraie moyenne, dont la valeur estimée correspond à la moyenne empirique des 10000 moyennes issues des échantillons de bootstrap. L’estimateur ainsi obtenu est alors plus robuste que la moyenne empirique sur l’échantillon initial.
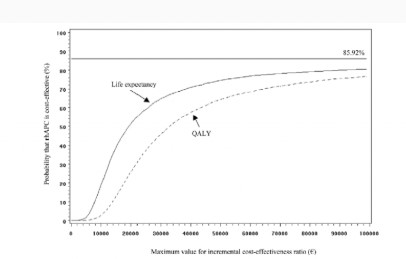
L’incertitude ne doit pas empêcher le décideur d’agir. Il est donc amené à prendre conjointement deux décisions. Dans un premier temps, il doit estimer quelles sont les chances que l’innovation rapporte plus qu’elle ne coûte en termes de santé publique, autrement dit quelles sont les chances qu’elle contribue plus à l’amélioration de l’état de santé de la population qu’elle ne risque de l’altérer du fait des ressources qu’elle accapare au détriment d’autres priorités sanitaires, dans un environnement financièrement contraint; Dans un second temps, il conviendra de réduire cette incertitude, en recherchant certes de nouvelles preuves, mais aussi en s’interrogeant sur leurs apports et leurs coûts respectifs, les schémas d’études à privilégier, le nombre de sujets nécessaires bref en mobilisant les théorie de la valeur de l’information. L’outil de cette démarche itérative est la courbe d’acceptabilité.
La courbe d’acceptabilité retrace le nombre de fois où la stratégie évaluée est jugée efficiente par rapport à son comparateur, sur l’ensemble des simulations effectuées par bootstrap pour un niveau donné de l’effort social consenti. On pourrait la désigner de façon plus informelle, sous le nom de « courbe des proportions de cas gagnants (CPCG) ». En faisant varier la valeur de l’effort socialement acceptable λ sur un intervalle défini, on obtient une plage de rapports cout résultat jugés efficients au regard de la volonté de payer collective.
La courbe est une autre manière de représenter en deux dimensions les résultats obtenus bootstrap dans le plan cout efficacité à quatre quadrants. Ainsi, la présence de points dans le quadrant Nord-Ouest (ΔE < 0 ;ΔC > 0) explique le fait que l’asymptote de la courbe d’acceptabilité ne soit pas égale à 1 : 14.08 % des points étant positionnés dans ce quadrant, l’asymptote vaut 0.86. Par ailleurs, plus le nuage est étiré (i.e., plus l’incertitude est grande sur l’efficacité), plus la courbe met de temps à atteindre son asymptote. D’un autre côté, lorsque la volonté de payer fait totalement défaut, alors ne sont jugés comme acceptables, que les traitements qui sont à la fois plus efficaces et moins chers que leur comparateur, c’est-à-dire ceux pour lesquels l’ordonnée à l’origine est strictement positive puisqu’ils se situent dans le quadrant Sud-Est du plan coût-efficacité.

La Courbe des Proportions de Cas Gagnants (CPCG) indique quels sont les chances d’avoir raison ou les risques d’avoir tort lorsqu’une stratégie est déclarée efficiente par rapport à son comparateur pour un niveau donné de l’effort socialement acceptable. Or le but recherché par un haut fonctionnaire de la santé est de maximiser l’état de la santé de la population dont il est responsable, beaucoup plus que de savoir quel est le degré d’incertitude associée à sa décision. Le choix de la meilleure stratégie thérapeutique ou du meilleur programme de santé publique ne repose pas sur la minimisation de l’incertitude, mais sur la maximisation du bénéfice collectif net entendu comme la différence entre le bénéfice clinique valorisé sur la base de l’effort social jugé acceptable et le coût qui lui est associé. Seules les stratégies qui répondent à ce critère pour chaque valeur de l’effort financier socialement acceptable sont susceptibles d’être retenues. La Frontière des Choix Appropriés multioptions (FDCA) est le lieu géométrique des points qui remplissent cette propriété. Contrairement aux CPCG, la frontière évalue la probabilité que le traitement soit efficient pour différentes valeurs de λ, dans le seul cas où celles-ci permettent de maximiser simultanément le bénéfice net moyen. Les options optimales étant les seules options représentées, le tracé de la FDCA ne correspond pas toujours aux interventions pour lesquelles la probabilité d’être coût efficace soit la plus élevée (Barton et coll., 2008)
L’analyse d’impact budgétaire compare deux situations : le coût de l’arsenal thérapeutique déjà existant, et celui d’un arsenal thérapeutique enrichi par l’arrivée d’un nouveau produit. Une analyse désagrégée par produit du type de celle faite dans les études coût-efficacité, exige de refaire tourner le modèle branche par branche pour procéder aux comparaisons face face dont les industriels souhaiteraient disposer.
L’analyse d’impact budgétaire s’intéresse à la prise en charge de la population cible : les soins concernent aussi bien les nouveaux malades que les anciens. La combinaison des entrées (date de début du traitement) et des sorties (date de décès) permet de représenter l’évolution de la population traitée dans le cadre d’un modèle ouvert multi-générationnel. Les modèles d’analyse coût-efficacité sont au contraire des modèles de cohorte fermée, qui suivent dans le temps le devenir d’une cohorte mono générationnelle dont les effectifs diminuent progressivement du simple fait des décès.
Chaque nouvelle cohorte débutant à l’instant t inclut les patients ayant reçu leur premier traitement à cette date. La taille de leurs effectifs respectifs est définie en fonction des hypothèses sur les taux de pénétration sur le marché. Ces cohortes « de nouveaux cas incidents » se surajoutent aux cohortes de cas anciens (« les cohortes prévalentes»), qui sont datées en fonction du mois et de l’année où les cas prévalents ont débuté leur traitement dans le passé. Les effectifs des cohortes diminuent au cours du temps en fonction des taux de décès retenus.

Les valeurs manquantes ne sont jamais les bienvenues dans une analyse statistique. Toutefois, selon leur ampleur et l’utilisation que l’on souhaite faire de variables concernées, le problème se pose différemment. En effet, si l’objectif est d’inclure de nombreuses variables, non complètes, dans une analyse multivariée, l’analyse perd en puissance, puisque chaque individu présentant une valeur manquante sur l’une des variables incluses est éliminé de l’analyse. Afin de ne pas perdre ces individus, il convient d’imputer une valeur là où la variable est manquante. La question est : quelle valeur ? Une des méthodes les plus simples consiste à imputer par la moyenne, mais cette méthode a le défaut de sous estimer la variabilité de la variable complétée. L’imputation multiple permet quant à elle de générer plusieurs jeux plausibles de données complètes (5 en général) à partir des données incomplètes initialement observées. Dans chaque jeu, chaque valeur manquante est imputée conditionnellement aux autres variables observées pour l’individu, par un modèle de régression. Plusieurs valeurs sont donc disponibles pour chaque valeur manquante. La valeur imputée au final correspond à leur moyenne. D’autre part, la variance du critère étudié tient compte à la fois de la variance intra-imputation (à l’intérieur d’un même jeu de données) et de la variance inter-imputation (entre les jeux de données générés). Ceci traduit donc l’incertitude associée à la valeur imputée.
Les études observationnelles se caractérisant par une absence de plan expérimental, elles sont susceptibles de présenter des biais de recrutement. La méthode d’appariement sur les scores de propension permet de les réduire. En effet, le score de propension désigne la probabilité, pour une personne de caractéristiques données, d’être exposée à un traitement. La distribution de ce score sur les groupes de traitement comparés fournit un critère de jugement de la comparabilité entre ces deux groupes : si biais de recrutement il y a, les scores auront tendance à être élevés pour les patients exposés et faibles pour les non exposés. Afin de neutraliser ces biais au maximum, un sous-échantillon de patients comparables entre les deux groupes peut être élaboré, par appariement sur les scores de propension : chaque patient exposé est apparié au patient non exposé ayant le score le plus proche, à condition que la différence entre les deux scores de soit pas trop grande. Ce sous-échantillon possède des caractéristiques proches de l’essai clinique, toutefois, il ne permet pas d’assurer la comparabilité sur les caractéristiques non observées.